Exhaustive Search, Branch And Bound Method And Greedy Algorithm To Solve Machine Layout Problem

Exhaustive search

The following steps show that how exhaustive search can be used to find out the solution of machine layout problem.

Step 1: Explore all possible paths in the tree using breadth first search. In our case all possible paths means all possible layouts of machines.

Step 2: Evaluate objective function for each possible path. Our objective function is to minimize total distance travelled by all parts.

Step 3: Return the best path. In other word, return best layout of machines which have minimum objective function value.

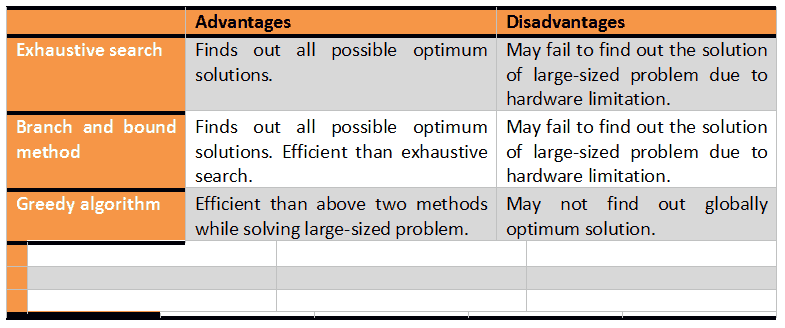
Exhaustive search is one of the exact solution methods. So it always finds out all possible optimum solutions. But time complexity of exhaustive search is very high.

If we have m machines then the number of different layouts among them is m! that is m x (m-1) x (m-2) x ….1. Exhaustive search is recommended to solve small-sized machine layout problems because it may fail to find out the solution of large-sized machine layout problem due to hardware limitation.

Consider we have only 25 machines then the number of different layouts among them is 25! & 25! = 1.5 x 10^25 approximately. If exhaustive search can examine 108 layouts per second then it will take just about 1.5 x 10^25/ 10^8 = 1.5 x 10^17 seconds to solve machine layout problem. Thus exhaustive search will take over 4.75 x 10^9 years to solve machine layout problem. This phenomenon is called combinatorial explosion.

Branch and bound method

The following steps show that how branch and bound method can be used to find out the solution of machine layout problem.

Step 1: Generates layouts of machines one at a time, keeping track of the best layout of machines found so far. Objective function value of the best layout of machines found so far is used as a bound on future layouts of machines.

Step 2: Examines each partially completed layout of machines and compare that branch with the bound, if objective function value of branch is found greater than the objective function value of bound then eliminates that branch including all of its possible successors.

Branch and bound method always finds out all possible optimum solutions and it is efficient than exhaustive search because it finds out the solution of machine layout problem in an exponential time. In the worst case branch and bound method may not cut any branches off the tree wasting all the additional work of comparing the branches with that worst bound at each node. Branch and bound method is still insufficient for solving the large-sized machine layout problems.

Greedy algorithm

Step 1: Randomly select a machine and call it a current machine.

Step 2: Select next machine such that the frequency of movement of parts between current machine and next machine is maximum.

Step 3: Declare newly selected next machine as a current machine.

Step 4: Repeat step 2 and 3 until all machines have been selected.

Greedy algorithm is a heuristic so it may not find out optimum solution of machine layout problem. It may sometimes find out the solution that is very far from globally optimum solution because it selects locally optimum alternative at each step. Greedy algorithm is efficient than previous two methods because it finds out the solution of machine layout problem in a polynomial time.

Table 1 presents the advantages and disadvantages of exhaustive search, branch and bound method and greedy algorithm.

Table 1: Advantages and disadvantages of exhaustive search, branch and bound method and greedy algorithm

Meta-heuristics such as genetic algorithm, simulated annealing, ant colony optimization and tabu search can be used to find out optimum or near optimum solution of large-sized machine layout problem within a reasonable amount of time.