Hypothesis Testing is a statistical method to infer and validate the significance of any assumption on a given data. While discussing about statistical significance of a data, it means that the data can be scientifically tested and determined on its significance against the predicted outcome. A detailed explanation given below will shed more information.
The data/information does not reveal the truth or is ambiguous at the first glance and require a prediction based on wisdom.
To start with, Hypothesis testing should follow the below steps:
-
Hypothesis Selection: The prediction based on wisdom is then considered as Null Hypothesis (H0). Say H0 = x, H0<x, and H0> x. The alternate hypothesis (Ha) should be such that it can be accepted or is unpredictable at the end of the test. For the above H0 given, the respective alternate hypothesis would be: Ha≠x, Ha≥ x and Ha≤ x.
Both the hypothesis are never rejected. It should always be: Accepted or Failed to accept either of the hypothesis (Refer the forthcoming example) -
Set the Significance Levels: It is quite probable that there may be an incorrect decision on accepting hypothesis (H0/Ha). Two types of error can occur which are:
- H0 is true but Ha is accepted due to error in the data (α Error)
- Ha is true but H0 is accepted due to some error in the data (β Error)
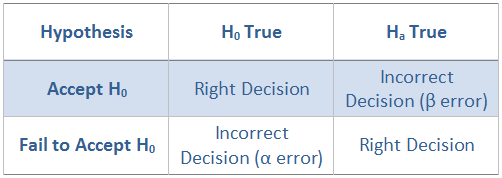
The ‘α error’ is also known as Type I error and ‘β error’ as Type II Error. Various tests are available that can be used to check the significance of the data depending on the hypothesis. Few of the tests are ANOVA, Chi-Square test, One and Two sample t-test, etc.
Both the cases would result in incorrect inference causing us to take wrong decision and there by not achieving the desired results. To overcome that the test should be:
- Fixed with an acceptable significance level (1- α value). Say 95% or 99%. It means a variation or error in the test results of around (α): 5% or 1% is allowable. Higher the significance level, more accurate is the test result.
- Increase the sample size which will reduce the β error
Adequate care should be taken in defining the H0 and Ha. The ‘α error’ threshold should be clearly defined and compared with appropriate probabilistic value which would determine whether to accept H0 or not.
- Conduct the Test: Select the appropriate test and state the relevant test statistic based on the data type and distribution. Then calculate the test statistic and arrive at the probability table value of the statistic based on the given degrees of freedom and significance level. For example: In a chi-square test, an Actual Chi-square value will be calculated through the formulas; An expected Chi-square value will be looked up from the Probability table corresponding to the given degrees of freedom and significance level.
-
Interpret the Results:
- Compare the actual and expected values and choose whether the Alternate Hypothesis can be accepted or not. (Refer to the respective Test for more details)
- Now from the statistically computed information check if the p-value (Probability value of error or variation) is less than the α value.
- p – Value < α value: Accept Alternate Hypothesis
- p – Value > α value: Reject Alternate Hypothesis
This is a purely probability based derivation and hence it is quite possible that different statistical tests may indicate different results.
Illustration: Now let us look at a world famous example which would help us in understanding hypothesis testing way clearer.
In a courtroom for a criminal trial, the defendant (Data point/observation) is not considered guilty unless proved.
Here,
H0: Defendant not guilty
Ha: Defendant guilty
According to the law we know that an innocent should never be acquitted unless otherwise it is proved to be. Here we have considered H0 as not guilty so that the erroneous decision of convicting an innocent is reduced. The alternate hypothesis would be accepted only when significant data is available to prove the defendant guilty.
When we have an innocent defendant and he is proved not guilty we accept the hypothesis H0) of wisdom whereas when we prove the defendant to be guilty we either fail to accept the H0or simply accept the alternate hypothesis.
The Hypothesis Testing is indeed a very powerful statistical method and can provide support to the information that you can intend to prove to be either correct or incorrect.
